|
|
|
|
|
|
7.17 Proposition Suppose a and b are reals in 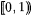 . . |
|
|
|
|
|
|
|
|
(a) 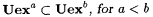 . . |
|
|
|
|
|
|
|
|
(b) 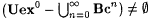 . . |
|
|
|
|
|
|
|
|
(c) 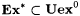 . . |
|
|
|
|
|
|
|
|
(d) 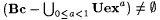 . . |
|
|
|
|
|
|
|
|
(e) 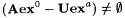 . . |
|
|
|
|
|
|
|
|
(f) 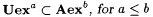 . . |
|
|
|
|
|
|
|
|
(g)  . . |
|
|
|
|
|
|
|
|
Proof: For parts (a) through (d) adapt the proofs of the analogous results in the previous section. |
|
|
|
|
|
|
|
|
For part (e), first let 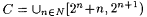 and and 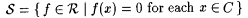 . It is straightforward that . It is straightforward that 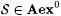 but that, for each but that, for each  , , 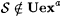 . . |
|
|
|
|
|
|
|
|
Part (f) follows from part (e). |
|
|
|
|
|
|
|
|
To show part (g), first fix rationals q and r with 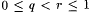 and let and let 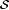 be as in Lemma 7.9. Clearly, be as in Lemma 7.9. Clearly, 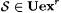 . By the argument of Lemma 7.9, . By the argument of Lemma 7.9, 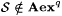 . Therefore, . Therefore, 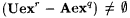 , and thus part (g) follows by the density of the rationals in the reals. , and thus part (g) follows by the density of the rationals in the reals. |
|
|
|
|
|
|
|
|
Thus, as might have been expected, the Uex hierarchy turns out to be a stricter version of the Aex hierarchy. The formulation of the text version of the Uex criteria and the proof of the analog of Proposition 7.17 are both straightforward and left to the reader. |
|
|
|
|
|
|
|
|
Uex is an improvement over Aex, but it fails to capture every aspect of uniform density. Consider the following example. For each  , let , let |
|
|
|
|
|
|
|
|
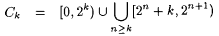 , , |
|
|
|
|
|
|
|
|
let gk be the characteristic function of 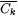 , let z = l x.0, and, finally, let M be such that on every input, M produces some fixed index for z. Clearly, for each k, ud(Ck) = 1 and aud(z, gk) = 0. Hence, M Uex0-identifies every element of , let z = l x.0, and, finally, let M be such that on every input, M produces some fixed index for z. Clearly, for each k, ud(Ck) = 1 and aud(z, gk) = 0. Hence, M Uex0-identifies every element of 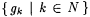 . But, for each k0, for all but finitely many k, the set . But, for each k0, for all but finitely many k, the set 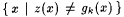 contains intervals of length k0 or greater. Thus M fails to give uniformly good approximations across the class contains intervals of length k0 or greater. Thus M fails to give uniformly good approximations across the class 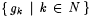 . The Huex (for homogeneous uniform approximate explanatory identification) criteria, developed in the next definition, address this problem. . The Huex (for homogeneous uniform approximate explanatory identification) criteria, developed in the next definition, address this problem. |
|
|
|
|