|
|
|
|
|
|
6-13 Show the following refinements of the observation in Exercise 6-12. |
|
|
|
|
|
|
|
|
(a) 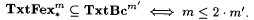 |
|
|
|
|
|
|
|
|
(b) 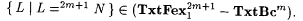 |
|
|
|
|
|
|
|
|
6-14 (Advanced) Consider the following variation on 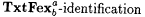 |
|
|
|
 |
|
|
|
|
6.35 Definition (Osherson, Stob, and Weinstein [140] )Let 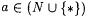 and and 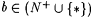 . . |
|
|
|
 |
|
|
|
|
(a) 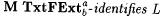 (written: (written: 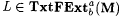 ) just in case for each text T for L there is a finite, nonempty set D of cardinality at most b such that (i) M finitely converges to D, (ii) for each ) just in case for each text T for L there is a finite, nonempty set D of cardinality at most b such that (i) M finitely converges to D, (ii) for each 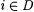 , Wi = a L, and (iii) for all i, , Wi = a L, and (iii) for all i,  , Wi = Wj , Wi = Wj |
|
|
|
 |
|
|
|
|
(b) 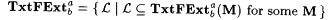 |
|
|
|
|
|
|
|
|
Show that for all 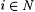 , ,  |
|
|
|
|
|
|
|
|
Open Question: Is 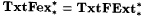 ? ? |
|
|
|
|
|
|
|
|
6-15 Two approaches to relaxing the strict requirement of Ex-identification have been considered in this chapter, namely, allowing anomalies in the final program and weakening the notion of convergence. Here we consider a third approach. Instead requiring convergence to a program for the function, we allow a scientist to converge to a "trial and error" procedure for the function. We formalize what we mean by a "trial and error" procedure for a function through programs for limiting approximations. A two argument j -program i is referred to as Lim-program for h just in case for all x 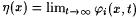 , where h (x) is undefined just in case the limit fails to exist. Intuitively, such a Lim-program, on a given input, is allowed finitely many mind changes about what output to produce. The next definition introduces a paradigm in which the scientist converges to a Lim-program for a finite variant of the function to be identified. , where h (x) is undefined just in case the limit fails to exist. Intuitively, such a Lim-program, on a given input, is allowed finitely many mind changes about what output to produce. The next definition introduces a paradigm in which the scientist converges to a Lim-program for a finite variant of the function to be identified. |
|
|
|
 |
|
|
|
|
6.36 Definition (Case, Jain, and Sharma [29]) Let  |
|
|
|
 |
|
|
|
|
(a) M LimEXa-identifies 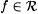 (written: (written: 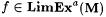 ) just in case ) just in case 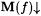 and M(f) is a Lim-program for an a-variant of f. and M(f) is a Lim-program for an a-variant of f. |
|
|
|
 |
|
|
|
|
(b) 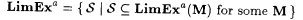 . . |
|
|
|
|