|
|
|
|
|
|
Case 1: Each stage terminates. Then, 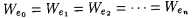 . Let . Let 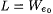 . Let . Let  . Clearly, T is a text for L and . Clearly, T is a text for L and 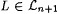 , but M on T does not finitely converge to a set of cardinality at most n. Hence, M does not , but M on T does not finitely converge to a set of cardinality at most n. Hence, M does not 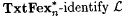 |
|
|
|
|
|
|
|
|
Case 2: Some stage s starts but fails to terminate. For each 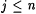 , let , let 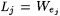 . Clearly, for each . Clearly, for each 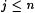 , , 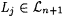 and and 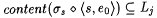 . Since the search in b fails in stage s, for every . Since the search in b fails in stage s, for every  extending extending  such that such that 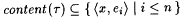 , we have , we have 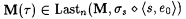 . Moreover, for each . Moreover, for each  , Lj D Lj, is infinite. Thus, there is a , Lj D Lj, is infinite. Thus, there is a 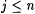 such that, for all such that, for all 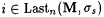 , Lj D Wi is infinite. Thus, M fails to , Lj D Wi is infinite. Thus, M fails to 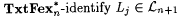 . . |
|
|
|
|
|
|
|
|
The above two cases imply the proposition. |
|
|
|
|
|
|
|
|
In contrast to the above result, part (a) of the next proposition shows that there are collections of languages for which an (m+ 1)-error index can be identified in the limit, but for which m-error indexes cannot be learned even if the scientist is allowed to vacillate among a finite, but unbounded, number of conjectures. |
|
|
|
|
|
|
|
|
(a) For 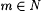 , , 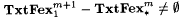 . . |
|
|
|
|
|
|
|
|
(b)For all 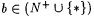 , , 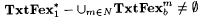 |
|
|
|
|
|
|
|
|
Proof: We prove only part (a). The proof of part (b) is left to the reader. |
|
|
|
|
|
|
|
|
Recall that 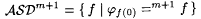 and that, by Proposition 6.5, and that, by Proposition 6.5, 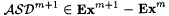 . Let Lf and . Let Lf and 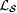 be as in the proof of Proposition 6.19. Consider the collection of single-valued total languages be as in the proof of Proposition 6.19. Consider the collection of single-valued total languages 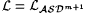 . . |
|
|
|
|
|
|
|
|
It is easy to see that 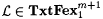 . We argue that . We argue that 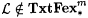 . Suppose by way of contradiction . Suppose by way of contradiction 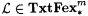 . Then, in a way similar to the proof of Proposition 6.19 it can shown that there exists a scientist that Fexm-identifies . Then, in a way similar to the proof of Proposition 6.19 it can shown that there exists a scientist that Fexm-identifies 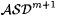 . But Fexm = Exm by Proposition 6.17. Hence, . But Fexm = Exm by Proposition 6.17. Hence, 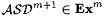 , a contradiction. , a contradiction. |
|
|
|
|
|
|
|
|
Exercises 6-12 and 6-13 below contain additional results comparing TxtFex with TxtBc. |
|
|
|
|
|
|
|
|
Errors in the final hypothesis for function identification were first considered by Blum and Blum [18] and later investigated extensively by Case and Smith [35]. The terminology |
|
|
|
|