|
|
|
|
|
|
6.14 Corollary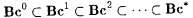 . . |
|
|
|
|
|
|
|
|
Proof (of Proposition 6.13): Proof for part (a). Fix an 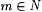 . Define . Define |
|
|
|
|
|
|
|
|
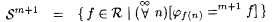 . . |
|
|
|
|
|
|
|
|
Clearly,  . We show that . We show that  . . |
|
|
|
|
|
|
|
|
Fix an arbitrary scientist M. We argue that M fails to Bcm-identify some 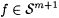 . Without loss of generality, assume that M is a total scientist. . Without loss of generality, assume that M is a total scientist. |
|
|
|
|
|
|
|
|
By implicit use of the operator recursion theorem (Theorem 2.6), we describe a repetition-free r.e. sequence of programs p(0), p(1), p(2), . . . such that, for some i, 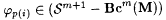 . Here is an informal effective construction of the j p(i)'s. . Here is an informal effective construction of the j p(i)'s. |
|
|
|
|
|
|
|
|
For each 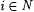 , , 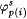 denotes the part of j p(i) defined before stage s. Let xs denote the least x such that j p(0)(xs) has not been defined before stage s. If the construction reaches stage s, then the domain of denotes the part of j p(i) defined before stage s. Let xs denote the least x such that j p(0)(xs) has not been defined before stage s. If the construction reaches stage s, then the domain of 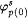 will be { 0, . . ., xs - 1 }, a finite initial segment of N, and will be { 0, . . ., xs - 1 }, a finite initial segment of N, and 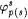 will be completely undefined. For each will be completely undefined. For each 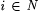 , set , set 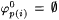 . Go to stage 0. . Go to stage 0. |
|
|
|
|
|
|
|
|
For each x << xs, set j p(s)(x) = j p(0)(x). |
|
|
|
|
|
|
|
|
Dovetail between a and b until, if ever, the search in b succeeds. |
|
|
|
 |
|
|
|
|
a. For i = 0 to  , set j p(s)(xs + i) = p(s). , set j p(s)(xs + i) = p(s).
b. Search for n, y0, y1, . . . ,ym such that 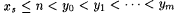 and, for each and, for each 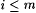 , ,  , where , where 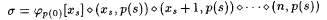 . . |
|
|
|
|
|
|
|
|
If and when the search in b succeeds, let y0, y1, . . ., ym be the m+1 points on which M's conjecture on evidential state 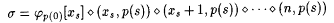 converges. converges. |
|
|
|
|
|
|
|
|
( We now force j p(0) to differ from M's conjecture on these m + 1 points. ) |
|
|
|
|
|
|
|
|
Let x be the maximum element on which j p(s) has been thus far defined and let x' = max({ x, ym }). |
|
|
|
|
|
|
|
|
For each 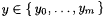 , set j p(0)(y) = p(0), if , set j p(0)(y) = p(0), if 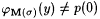 , and set j p(0)(y) = p(s), otherwise. , and set j p(0)(y) = p(s), otherwise. |
|
|
|
|
|
|
|
|
For each 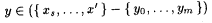 , set j p(0)(y) = p(s). , set j p(0)(y) = p(s). |
|
|
|
|
|
|
|
|
For each 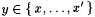 , set j p(s)(y) = p(s). , set j p(s)(y) = p(s). |
|
|
|
|
|
|
|
|
( Note that at this point in the definitions of j p(0) and j p(s), these two functions are (m + 1)-variants. ) |
|
|
|
|