|
|
|
|
|
|
In Chapter 5 we considered several conceptions of "scientist." In the present chapter we examine alternative criteria of scientific success. |
|
|
|
|
|
|
|
|
The Ex and TxtEx paradigms require the learner's conjectures to converge to some one index for the function or language being learned. This models both the accuracy and stability of successful learning. However, not all theorists take such a requirement to be necessary for learning, although most accept its sufficiency. It is noted, for example, that physicists sometimes employ explanations that are predictively inaccurate for certain experiments. In particular, Newtonian mechanics was used for explanation long after it was recognized that the theory failed to accurately predict dispersion in the X-ray region. Similarly, in the developmental context it might be doubted that children stabilize to a grammar that exactly models the parents' language — or even stabilize to a single grammar at all. Accordingly, more liberal conceptions of accuracy and stability have been proposed for learning, enforcing weaker requirements in these respects. The present chapter reviews some elementary success criteria of this nature. More sophisticated criteria are discussed in Chapter 7. In each case we conceive of the new criterion as giving rise to a novel paradigm of inductive inference. In what follows, extensions of Ex are considered first, followed by extensions of TxtEx. |
|
|
|
|
|
|
|
|
§6.1 Criteria for Function DIidentification |
|
|
|
|
|
|
|
|
§6.1.1 Anomalous Ex-identification |
|
|
|
|
|
|
|
|
Our initial focus will be on relaxing the strict accuracy required for success within the paradigm Ex. One means of weakening this requirement is to define a proximity measure between functions, and then allow learners to converge to indexes that are for functions "sufficiently close" to the target. A simple proximity measure involves counting the number of points on which two functions give different results. For finite n we thus consider two functions to be "n-close" if they are equal on all but at most n arguments. (They are considered unequal on an argument if only one of them is defined there.) Two functions are called "finitely" close if they are n-close for some n. These ideas are formalized in the following definition, which is recalled from Chapter 2. |
|
|
|
|
|
|
|
|
6.1 Definition Let 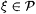 , , 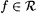 , and , and 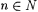 . . |
|
|
|
|