Tableaux
Our formal model of entailment judgments (isValidProp) has a very
‘semantic’ flavor to it. It computes what we as trained linguists
might think of as the ‘meaning’ of a term (a function from situations
to truth values), and then tests that the term is true in every
situation. The way it tests that a term is true in every situation is
to systematically generate all the situations that differ from one
another only in the truth values they assign to the atomic
propositions occurring in the term, which it does by computing the
powerset of the set of all of these atomic propositions.
A fundamental observation, going back to antiquity, is that meaning is mirrored in form. This allows us to do semantic-y things by manipulating syntactic objects. Well-behaved logics have the property that syntactic manipulation allows you to simulate semantics perfectly; soundness theorems tell us that syntactic manipulation (proof procedures) are faithful to semantics, and completeness theorems tell us that syntactic manipulation can allow us to do everything that we want.1
There are many different syntactic methods, even for propositional logic, which attempt to establish the validity (truth in all situations) of a sequent/formula. The one that we’ll look at is the system of semantic tableaux. Hilbert proof systems use axioms (syntactic transformations) to obtain conclusions from premises, in the hope of obtaining the conclusion of a sequent from its antecedents. As the axioms are known to preserve truth (they are sound), if you can transform the antecedents into the consequent in this way you have succeded in demonstrating that any situation in which the antecedents are true is one in which the conclusion is true as well. If a proof cannot be constructed, the sequent is not valid (as the proof system is complete), which means that there is some situation in which the sequent is false. We can think of the tableau method as turning this on its head: it tries to construct situations in which the sequent holds. If it can, then it is satisfiable, which means that its negation is false is at least one situation, and thus invalid. If it cannot, then its negation is true in every situation, and is thus valid. Because of this, the tableau method is used as a refutation procedure; to determine whether a sequent is valid, one applies the tableau method to its negation, and sees whether the negation can ever be true.
TL/DR
Please practice using the tableau method!
- Create a tableau starting with the following signed formulae:
-
\(\textbf{T}: p \vee \neg p\)
-
\(\textbf{F}: p \vee \neg p\)
-
\(\textbf{T}: (p \vee \neg q) \wedge (q \vee \neg r) \wedge (\neg p \vee r) \)
remember that conjunction is associative: you get the same truth value no matter how you parenthesize the following expression. \[p \wedge q \wedge r\ \approx\ p \wedge (q \wedge r) \equiv (p \wedge q) \wedge r\]
-
\(\textbf{F}: (p \vee \neg q) \wedge (q \vee \neg r) \wedge (\neg p \vee r) \)
-
- I claim that the following formulae are valid. Verify my claims using the tableau method!
- \(\neg (p \wedge \neg p)\)
- \(\neg (\neg p \vee q) \vee \neg (p \wedge \neg q)\)
- \(\neg ((\neg p \vee q) \wedge (p \wedge \neg q))\)
Here is a more conceptual question.
-
What should tableau rules for the implication connective look like? (i.e., how should we construct tableaus for formulae like \(p \rightarrow q\)?)
the truth table for implication looks as follows:
\(p\) \(q\) \(p \rightarrow q\) 1 1 1 1 0 0 0 1 1 0 0 1
Tableaux
We have been viewing situations as specifications of which atomic sentences they make true, but of course, if we know which atomic sentences are true in a situation, we also know (or can figure out) which complex sentences are true in that situation. When trying to determine whether a formula can be true, we find ourselves in the opposite setting! Here we are given a formula, told that it is true in some mysterious situation, and are given the task of trying to discover exactly which situation this is! Take as an example the formula \(p_{1} \wedge \neg (p_1 \wedge \neg p_{2})\). We are tasked with constructing a situation in which this formula is true. How should we proceed? We can let ourselves be guided by the syntactic form of the formula. We know that a conjunction is true only if both conjuncts are true. Thus, in our mysterious situation, both \(p_{1}\) and \(\neg (p_{1} \wedge \neg p_{2})\) must be true. As the first conjunct, \(p_{1}\), is an atomic sentence, we have learned that the situation we are after must be one in which \(p_{1}\) is true. The second conjunct, \(\neg (p_{1} \wedge \neg p_{2})\), must be true as well. We let ourselves again be guided by its syntactic form, which is that of a negation. A negated sentence is true, only if the sentence negated is false. Thus our situation must make \(p_{1} \wedge \neg p_{2}\) false. A conjunction, although true only when both conjuncts are true, can be false in multiple ways: here either \(p_{1}\) must be false, or \(\neg p_{2}\) must be false (or both). As we have already learned that \(p_{1}\) must be true, we cannot also let it be false. Therefore, we must let \(\neg p_{2}\) be false. Guided again by the syntactic form of this sentence, we reason that it, as a negated sentence, can be false only if \(p_{2}\) is true. We now have resolved the identity of our mystery situation: it makes both \(p_{1}\) and \(p_{2}\) true. We can view this reasoning as a tree.
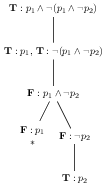
Figure 1: Our tableau example in tree form
In this tree, we indicate on each formula whether it is true (T) or false (F) in the situation(s) we are constructing. We call a formula with such an indication of its truth a signed formula. At each node of the tree, we write down the new information we have gained about the situation(s) we are constructing. A situation is given by following a path from the root to a leaf; that situation is one which maps each formula on the path to the truth value it is indicated as having. Some situations are impossible (they would make a single formula both true and false). This is marked by an asterisk under the leaf.
We can present our informal reasoning more precisely if we think for a moment in terms of tableaux trees (as in the figure). We begin with a single formula, and we will construct a tree from it using the following rules.
- \(\textbf{T}: \neg\phi\)
- create a single daughter, with signed formula \(\textbf{F}: \phi\)
- \(\textbf{F}: \neg\phi\)
- create a single daughter, with signed formula \(\textbf{T}: \phi\)
- \(\textbf{T}: \phi \wedge \psi\)
- create a single daughter, with signed formulae \(\textbf{T}: \phi\) and \(\textbf{T}:\psi\)
- \(\textbf{F}: \phi \wedge \psi\)
- create two daughters, one with signed formula \(\textbf{F}:\phi\) and the other with signed formula \(\textbf{F}:\psi\)
- \(\textbf{T}: \phi \vee \psi\)
- create two daughters, one with signed formula \(\textbf{T}:\phi\) and the other with signed formula \(\textbf{T}:\psi\)
- \(\textbf{F}: \phi \vee \psi\)
- create a single daughter, with signed formulae \(\textbf{F}: \phi\) and \(\textbf{F}:\psi\)
Each step in our informal reasoning corresponds to one of the rules presented here. For example, when we began with the assumption that \(p_{1} \wedge \neg (p_1 \wedge \neg p_{2})\) was true, and reasoned that this could only happen if the situation made both conjuncts true, we informally applied the rule operating on true conjuncts: from \(\textbf{T}:\phi \wedge \psi\) add \(\textbf{T}:\phi\) and \(\textbf{T}:\psi\). To be more precise, we need first some ancillary notions. The Tableau method is essentially constructing a set of situations. When we represent our work in tree form, each path from the root to a leaf represents one of these situations. In the tableaux literature the word branch is often used to mean a path from the root to a leaf. Each branch is a hypothesis about a possible situation which makes the formula we started with true. Sometimes we will end up with a branch representing an illegitimate situation, one which says the same formula is both true and false. A branch representing an illegitimate situation is called closed. A branch is closed just in case it contains both \(\textbf{T}:\phi\) and \(\textbf{F}:\phi\) for some formula \(\phi\). Finally, a non-atomic signed formula \(\textbf{S}:\phi\) is productive in a branch just in case it has not already been expanded.
With these definitions in mind, tableau expansion works in the following way. At each step, choose an open branch, and choose a productive formula. This formula will match exactly one of the six rules given above, which will tell us how to expand it. The nodes created by expanding a formula are added as daughters to the (unique) leaf of the branch.
We can work through a tableau proof for \(\neg(p_{1} \wedge \neg (p_1 \wedge \neg p_{2})) \vee p_{2}\). As the tableau method is a refutation system, we will try to construct a situation in which this formula is false. Thus, we begin with the tree below.
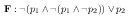
In this tableau, there is a single branch (path from leaf to root), because there is only one node which is both leaf and root. We choose to work on the only branch, and we try to expand the only formula. This formula is of the form \(\textbf{F}:\phi \vee \psi\), which is expanded by extending the branch with a single node containing two formulae. This is depicted below.

In this tableau, there is still just a single branch, but it contains two nodes. We choose this unique branch to work on. On this branch there is just one productive signed formula. The formula at the root is not productive (anymore), as we have already expanded it. The signed atomic formula at the leaf is not productive, because it is an atomic formula. We choose to expand the (only other) formula of the form \(\textbf{F}:\neg \phi\), which is expanded by extending the branch with a single node containing a single formula, as shown below.
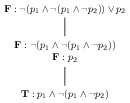
Again, there is but one branch, and one productive formula in this branch (the newly created one), of the form \(\textbf{T}:\phi \wedge \psi\). We expand it, extending the branch with a single node containing two formulae.

There continues to be a single branch, and of the two new formulae created in the last step, only one (of the form \(\textbf{T}:\neg \phi\)) is productive. We expand it, extending the branch with a single node containing single formula.
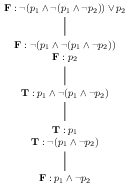
Again, we have just a single branch (although now it is of a respectable length), and just one productive formula (of the form \(\textbf{F}:\phi \wedge \psi\)). We expand it, extending the branch with two sister nodes, each containing a single formula.
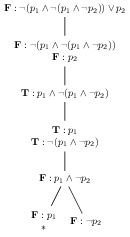
Of the two branches created, the one on the left in the tree (ending with the formula \(\textbf{F}:p_{1}\)) is closed; the branch contains both \(\textbf{F}:p_{1}\) (at the leaf) and \(\textbf{T}:p_{1}\) (two nodes above the leaf). This branch represents an illegitimate situation. The only remaining branch contains a single productive formula (the leaf of the form \(\textbf{F}:\neg \phi\)), which when expanded extends the branch with a single one-formula node.
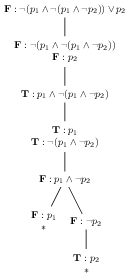
The newly extended branch is closed, as it contains both \(\textbf{T}:p_{2}\) (at the leaf) and \(\textbf{F}:p_{2}\) (at the daughter of the root). All branches of the tree are closed, and thus there is nothing more that we can do. Our tableau building has come to an end, and we did not succeed in creating a situation compatible with the falsity of the sentence \(\neg(p_{1} \wedge \neg (p_1 \wedge \neg p_{2})) \vee p_{2}\). Thus (because the tableau method is correct), the sentence is true in every situation, and is thus valid.
-
We need both together, as each individually can be trivially true. Soundness holds if we have no allowable syntactic manipulations: if we cannot do anything, then we of course can do nothing wrong. Completeness holds if our syntactic manipulations are free: if we can do anything at all, of course we can do everything that we want. ↩︎