Tableaux for Subjects and Predicates
Having extended the range of entailments we are able to correctly predict (by deepening our syntactic analysis of sentences so as to view previously ‘atomic’ sentences as being composed of subects and predicates), we should ask whether, and if so, how, we can derive these predictions proof-theoretically (i.e. syntactically).
We would like to extend the tableau method so as to treat sentences involving subjects and predicates. As our (meta-)language is modular, in the sense of having independent pieces for:
- logical operators at the sentential level
- logical operators at the predicate level
- subjects and predicates
we may focus our attention on each of these pieces individually. In that respect, our previous work on tableaux for boolean combinations of sentences was not wasted.
Tableau for simple sentences
We begin with tableaux for subjects and predicates, without any logical operators.
A tableau branch is intended to represent a (partial) situation, one which assigns the truth values indicated by the signs to the signed formulae occuring in it. When the expressions under investigation were uniformly proposition symbols (and boolean combinations thereof), our situations simply assigned truth values to atomic formuale. We have now, next to proposition denoting expressions, also individual denoting expressions, and functions from the latter to the former. Accordingly, our situations assign to individual denoting expressions individuals, and to property expressions sets thereof (or equivalently functions specifying which individuals the property is true of). Because a predicate is not true or false in a situation, but only true or false of a particular individual in a situation, we extend our repertoire of signs to include not just \(\mathbf{T}\) and \(\mathbf{F}\), but also \(\mathbf{X}\alpha\) for \(\mathbf{X}\) a truth value and \(\alpha\) a sequence of individuals. We will view a signed expression, \(\mathbf{X}\alpha : \phi\), to indicate that \(\phi\), when given arguments \(\alpha\), has truth value \(\mathbf{X}\). Our old notation for signed propositions, \(\mathbf{X}:\phi\), indicating that formula \(\phi\) has truth value \(\mathbf{X}\), is now understood as saying that expression \(\phi\) has truth value \(\mathbf{X}\) without being given any arguments at all.1 With this interpretation, we can see that the following rule is valid (truth-preserving).2
- shift argument
- \(\mathbf{X}\alpha : A\ B \mapsto \mathbf{X}\alpha{}B : A\)
Extracting a situation from a tableau
A tableau branch is closed if it contains both \(\mathbf{T}\alpha : A\) and \(\mathbf{F}\alpha : A\) for some expression \(A\) and arguments \(\alpha\). In this case, the tableau branch places contradictory demands on a possible situation.
Otherwise, a signed expression of the form \(\mathbf{X}s : p\), where \(s\) is a subject term and \(p\) a predicate term, is interpreted as stating that the situation does (if \(\mathbf{X} = \mathbf{T}\)) or does not (if \(\mathbf{X} = \mathbf{F}\)) assign an individual, which we for convenience also call \(s\), to the set denoted by the predicate \(p\).
For example, if our tableau branch contains the following signed
formulae: \(\{\mathbf{T}\textsf{john} : \textsf{dance},
\mathbf{F}\textsf{mary} : \textsf{sing}\}\), then it represents all
situations in which the individual ‘john’ is a dancer (\(\textsf{john}\in\textsf{dance}\)), and the individual ‘mary’ is not a singer (\(\textsf{mary}\notin \textsf{sing}\)).
Incorporating logical operators
Our tableau rules for the logical operators applied to sentences carries over without change to our (slightly) generalized notation:
- \(\mathbf{T} : \mathop{\textsf{not}}\phi\)
- \(\mathbf{F}: \phi\)
- \(\mathbf{F} : \mathop{\textsf{not}}\phi\)
- \(\mathbf{T}: \phi\)
- \(\mathbf{T} : \phi \mathrel{\textsf{and}} \psi\)
- \(\mathbf{T}: \phi\) and \(\mathbf{T} : \psi\) in the same branch
- \(\mathbf{F} : \phi \mathrel{\textsf{and}} \psi\)
- \(\mathbf{F}: \phi\) and \(\mathbf{F} : \psi\) in different branches
- \(\mathbf{T} : \phi \mathrel{\textsf{or}} \psi\)
- \(\mathbf{T}: \phi\) and \(\mathbf{T} : \psi\) in different branches
- \(\mathbf{F} : \phi \mathrel{\textsf{or}} \psi\)
- \(\mathbf{F}: \phi\) and \(\mathbf{F} : \psi\) in the same branch
We can reason about the tableaux rules we want for the logical operators applied to predicates by remembering that a signed formula \(\mathbf{X}s : p\) is interpreted as stating that the situation does (if \(\mathbf{X} = \mathbf{T}\)) or does not (if \(\mathbf{X} = \mathbf{F}\)) assign an individual, which we for convenience also call \(s\), to the set denoted by the predicate \(p\).
If the predicate is \(\mathop{\textsf{not}} p\), then, recalling that an individual \(x\) belongs to the set denoted by \(\mathop{\textsf{not}} p\) just in case \(x\) does not belong to the set denoted by \(p\) and vice versa, we can reason to the following rules for negated properties:
- \(\mathbf{T}s : \mathop{\textsf{not}} p\)
- \(\mathbf{F}s : p\)
- \(\mathbf{F}s : \mathop{\textsf{not}} p\)
- \(\mathbf{T}s : p\)
For the first rule, \(\mathbf{T}s : \mathop{\textsf{not}} p\) is understood as requiring a situation to put the individual s in the set \(\mathop{\textsf{not}} p\), which is equivalent to not putting the individual s in the set p, which is just what \(\mathbf{F}s : p\) says.
We can reason similarly in case the predicate is \(p \mathrel{\textsf{and}} q\), which is interpreted as the intersection of the sets p and q.
- \(\mathbf{T}s : p \mathrel{\textsf{and}} q\)
- \(\mathbf{T}s: p\) and \(\mathbf{T}s : q\) in the same branch
- \(\mathbf{F}s : p \mathrel{\textsf{and}} q\)
- \(\mathbf{F}s: p\) and \(\mathbf{F}s : q\) in different branches
For the first rule, \(\mathbf{T}s : p \mathrel{\textsf{and}} q\) requires a situation to put the individual s in the set \(p \mathrel{\textsf{and}} q\), which is equivalent to putting s in p and putting s in q, which is what is required by having both \(\mathbf{T}s: p\) and \(\mathbf{T}s : q\) in tAhe same branch. For the second rule, \(\mathbf{F}s : p \mathrel{\textsf{and}} q\) requires a situation not to put the individual s in the set \(p \mathrel{\textsf{and}} q\), which is equivalent to either not putting s in p or not putting s in q. These represent two potentially different situations, and so we bifurcate the current branch into two, one of which doesn’t put s in p (and so contains \(\mathbf{F}s: p\)), and the other doesn’t put s in q (and so contains \(\mathbf{T}s : q\)).
Finally, the disjunction of predicates is interpreted as their union.
- \(\mathbf{T}s : p \mathrel{\textsf{or}} q\)
- \(\mathbf{T}s: p\) and \(\mathbf{T}s : q\) in different branches
- \(\mathbf{F}s : p \mathrel{\textsf{or}} q\)
- \(\mathbf{F}s: p\) and \(\mathbf{F}s : q\) in the same branch
Comparing the rules for propsitions with those for predicates, we are struck by their similarity: they are the same, except for the individual attached to the sign! We can write a single, unified, rule for each signed term by abstracting over the arguments carried by the sign:
- \(\mathbf{T}\alpha : \mathop{\textsf{not}}\phi\)
- \(\mathbf{F}\alpha: \phi\)
- \(\mathbf{F}\alpha : \mathop{\textsf{not}}\phi\)
- \(\mathbf{T}\alpha: \phi\)
- \(\mathbf{T}\alpha : \phi \mathrel{\textsf{and}} \psi\)
- \(\mathbf{T}\alpha: \phi\) and \(\mathbf{T}\alpha : \psi\) in the same branch
- \(\mathbf{F}\alpha : \phi \mathrel{\textsf{and}} \psi\)
- \(\mathbf{F}\alpha: \phi\) and \(\mathbf{F}\alpha : \psi\) in different branches
- \(\mathbf{T}\alpha : \phi \mathrel{\textsf{or}} \psi\)
- \(\mathbf{T}\alpha: \phi\) and \(\mathbf{T}\alpha : \psi\) in different branches
- \(\mathbf{F}\alpha : \phi \mathrel{\textsf{or}} \psi\)
- \(\mathbf{F}\alpha: \phi\) and \(\mathbf{F}\alpha : \psi\) in the same branch
If \(\alpha\) is empty, we have the special case given for propositions, and if \(\alpha\) is a single individual, we have the special case given for predicates.
Some examples
We recognize3 that the sentences “John either doesn’t cry or laughs and doesn’t jump” and “John jumps” entails the sentence “It is not the case that John cries.”
We can use the tableau method to try to construct a counter-example for this entailment. A counter-example would have to make the premises true, and the conclusion false. Accordingly, we begin with the signed formulae \(\mathbf{T} : (\mathop{\textsf{not}} \textsf{cry} \mathrel{\textsf{or}} (\textsf{laugh} \mathrel{\textsf{and}} \mathop{\textsf{not}} \textsf{jump}))\ \textsf{john}\), \(\mathbf{T} : \textsf{jump}\ \textsf{john}\), and \(\mathbf{F} : \mathop{\textsf{not}} (\textsf{cry}\ \textsf{john})\) in our tableau.
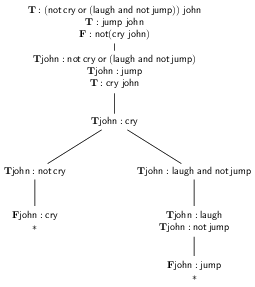
Figure 1: A closed tableau
As the tableau is closed, there is no situation in which the antecedent formulae are true and the conclusion formula false, whence in every situation in which the antecedent formulae are true, the conclusion formula is also true. Therefore, the entailment is valid.
We can partially repeat the previous tableau, asking this time what
situations are compatible with the truth of the antecedents. This
time we begin our tableau with the signed formulae \(\mathbf{T} :
(\mathop{\textsf{not}} \textsf{cry} \mathrel{\textsf{or}}
(\textsf{laugh} \mathrel{\textsf{and}} \mathop{\textsf{not}}
\textsf{jump}))\ \textsf{john}\) and \(\mathbf{T} : \textsf{jump}
\textsf{john}\).
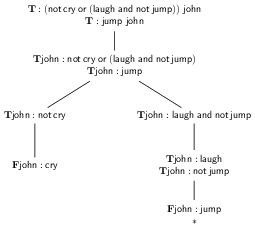
Figure 2: An open tableau
This tableau has one open branch, which represents a situation in which ‘john’ is a jumper (\(\textsf{john} \in \textsf{jump}\)) but not a crier (\(\textsf{john}\notin \textsf{cry}\)).
-
This is saying the same thing, of course. The point is that our old notation is compatible with this new interpretation. ↩︎
-
Thies rule is overkill, in the sense that our syntax currently only allows for an expression to have one argument (predicates take just one argument). I formulate it in this general sense in anticipation of having more arguments in the future. ↩︎
-
After some thought. ↩︎