Beilage III.

Die Bewegung gezupfter Saiten.
Zu Seite 90.

Es sei x die Entfernung eines Punktes einer Saite von ihrem einen Endpunkte, l die Länge der Saite, so daß für ihren einen Endpunkt x = 0, für den anderen x == l. Es genügt, den Fall zu untersuchen, wo die Saite in einer einzigen durch ihre Gleichgewichtslage gelegten Ebene hin und her schwingt. Es sei y die Entfernung des Punktes x aus der Gleichgewichtslage zur Zeit t; ferner sei m das Gewicht der Längeneinheit und S die Spannung der Saite, so sind die Bedingungen ihrer Bewegung

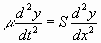.........................................................(1) und da die Enden der Saite als unbeweglich angenommen werden, muß. sein y = 0,


                    wenn x = 0 oder x = l .........................................................(1a)
 

 Das allgemeinste Integral der Gleichung (l), welches die Bedingungen. (1a) erfüllt, und einer periodischen Bewegung der Saite entspricht, ist folgendes :

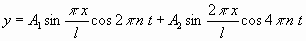
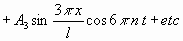
............(1b)

worin 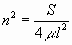und A1, A2, A3 sowie B1, B2, B3 etc. beliebige konstante Koeffizienten sind. Deren Größe kann bestimmt werden, wenn für einen bestimmten Wert von t Form und Geschwindigkeit der Saite bekannt sind.

Für den Zeitpunkt t = 0 wird die Form der Saite folgende:
 

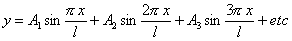...........................................(1c).

 

und deren Geschwindigkeit:

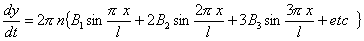............................(1d)

.


.

Denken wir uns nun, die Saite sei mit einem spitzen Stift zur Seite gezogen worden, und zur Zeit t = 0 habe man den Stift fortgezogen, sodaß in diesem Augenblick die Schwingungen begonnen haben, dann hat die Saite zur Zeit t = 0 keine Geschwindigkeit, und für jeden Wert von x ist 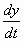= 0; dies kann aber nur der Fall sein, wenn in Gleichung (1d)

0 = B1 = B2 = B3 etc.

Die Koeffizienten A hängen von der Gestalt der Saite zur Zeit t = 0 ab. Die Saite mußte in dem Augenblick, wo der Stift sie losließ, die auf Seite 93 in Fig. 18 A dargestellte Form zweier gerader Linien haben, die von der Spitze des Stifts nach den beiden Befestigungspunkten der Saite gezogen sind. Nennen wir die Werte von x und y für den Saitenpunkt, an dem der Stift angriff, beziehlich a und b, so waren zur Zeit t = 0 die Werte von y wenn

                                                    a > x > 0

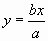......................................................................................(2)

 wenn l > x > a .................................................................................(2a) und es müssen die Werte von y aus (1c) und (2) oder beziehlich (2a) identisch werden.

Um den Koeffizienten Am zu finden verfährt man bekanntlich so, daß man beide Seiten der Gleichung (1c) mit sin dx multipliziert, und von x = 0 bis x = l integriert. Dann reduziert sich die Gleichung (1c) auf

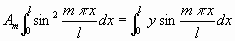........................................(2b) worin für y die Werte aus (2) und (2a) zu setzen sind. Wenn in (2b) die Integrationen ausgeführt werden, erhält man: 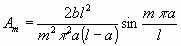......................................................(3) Es wird also Am gleich Null werden, und somit der mte Ton der Saite wegfallen, wenn 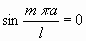, d. h. wenn a = 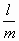 oder =  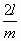oder =  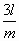etc. Denkt man sich also die Saite in m gleiche Teile geteilt, und in einem der Teilpunkte angeschlagen, so fällt ihr mter Ton weg, dessen Knotenpunkte auf die genannten Knotenpunkte fallen.

Jeder Knotenpunkt für den roten Ton ist auch Knotenpunkt für den 2 mten, 3 mten, 4 mten u. s. w., es fallen also auch alle die letzteren Töne gleichzeitig fort.

_________________

Man kann das Integral der Gleichung (l) bekanntlich auch in folgender Form darstellen:

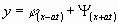..................................................................(4) wo , j und y aber willkürliche Funktionen sind. Die Funktion j(x-at) bedeutet eine beliebige Form der Saite, welche mit der Geschwindigkeit a, sonst aber ohne Veränderung, in Richtung der positiven x fortrückt, die andere Funktion y(x-at) eine ebensolche, die mit gleicher Geschwindigkeit in Richtung der negativen x fortrückt. Beide Funktionen muß man von x = - ¥ bis x = + ¥ gegeben denken für einen bestimmten Wert der Zeit, dann ist die Bewegung der Saite bestimmt.

Unsere Aufgabe, die Bewegung der gezupften Saite zu bestimmen, wird in dieser zweiten Form gelöst sein, wenn wir die Funktionen jund y so bestimmen können, daß

1) für die Werte x = 0 und x = l der Wert von y für jeden Wert von t konstant gleich 0 wird. Dies geschieht, wenn für jeden Werth von t

                                                            j( -at) = - y( + at) .................................................(4a)

j( l -at) = - y( l + at) ..............................................(4b) Setzen wir in der ersten Gleichung at = - v, in der zweiten l + at = - v, so erhalten wir jv = - y( - v)

j( 2l + v) = - y( - v)

 also j( 2l + v) = yv.......................................................(5) Die Funktion j ist also periodisch; sobald ihr Argument um 21 wächst, erhält sie wieder denselben Wert. Das Gleiche läßt sich ebenso für y finden.

2) Für t = 0 muß sein 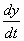= 0 zwischen den Werten x = 0 bis x = l.

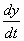Daraus folgt, wenn wir  mit y' bezeichnen, indem wir den Werth von  aus Gleichung (4) gleich Null setzen:

j’ (x) = y' (x) Wenn wir dies nach x integrieren : j x = y x + C Und da sich weder y noch 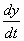 ändert, wenn wir zu jdieselbe Konstante addieren und von y abziehen, so ist die Konstante C vollkommen willkürlich, und wir können sie gleich Null setzen, also schreiben: j (x) = y (x) ........................................................(5a) 3) Da endlich zur Zeit t = 0 innerhalb x = 0 bis x = l die Größe y = j (x) + y (x) = 2j(x) den in Fig. 18 A dargestellten Wert haben soll, so geben die Ordinaten dieser Figur auch gleich den Wert von 2j (x) und von 2y (x) . gemäß Gleichung (5): zwischen x = 0 und x = l

zwischen x = 2l und x = 3l

zwischen x = 4 l und x = 5 l

 
u. s. w. Da dagegen aus (4a), (4b) und (5) folgt j( - v) = - j( v) und j( l - v) = - j( l + v) so ist der Wert von 2j (x) gegeben durch die Kurve Fig. 18 G zwischen x = - l und x = 0

zwischen x = - 3 l und x = - 2 l


und ebenso             zwischen x = l und x = 2 l

zwischen x = 31 und x = 4 l u. s. w. So sind die Funktionen j und y vollständig bestimmt, und indem man die durch beide dargestellten Wellenlinien mit der Geschwindigkeit a nach entgegengesetzten Richtungen fortschreiten läßt, erhält man die Saitenformen, welche in Fig. 18 abgebildet sind, und welche die Veränderungen der Saite nach je ein Zwölfteil ihrer Schwingungsdauer darstellen.