|
|
|
|
|
|
If 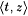 is ever found, then: is ever found, then:
 set set 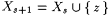 , ,
 set ys+1 to the least number of the form set ys+1 to the least number of the form  that is not in the finite set that is not in the finite set 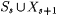 , ,
 set set 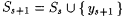 , ,
 set s s+1 be the least extension of s s such that content( s s+1) = Ss + 1, set s s+1 be the least extension of s s such that content( s s+1) = Ss + 1,
 set set 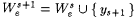 , and , and
 go to stage s + 1. go to stage s + 1. |
|
|
|
|
|
|
|
|
To show that M fails to accountably identify  , we consider two cases. , we consider two cases. |
|
|
|
|
|
|
|
|
Case 1: All stages of the construction halt. Let L = We. It is easy to see that 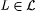 and and 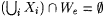 . Let . Let 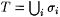 . Observe that T is a text for L. But for each i we have . Observe that T is a text for L. But for each i we have 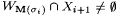 . Thus M fails to identify L. . Thus M fails to identify L. |
|
|
|
|
|
|
|
|
Case 2: Some stage s starts but does not halt. By Kleene's recursion theorem there exists an e' > e such that 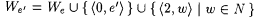 . Clearly, . Clearly, 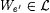 . However, . However,  . Thus, M fails to be accountable on We'. . Thus, M fails to be accountable on We'. |
|
|
|
|
|
|
|
|
The global version of accountability turns out to be more restrictive than the class version. To show this, let us first recall from Chapter 4 that 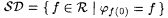 and introduce the following. and introduce the following. |
|
|
|
|
|
|
|
|
5.17 Definition 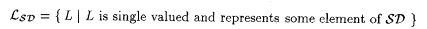 . . |
|
|
|
|
|
|
|
|
5.18 Proposition  . . |
|
|
|
|
|
|
|
|
Proof: We first show that 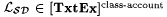 . By the S-m-n Theorem (Theorem 2.1), there is a recursive g such that, for all i, . By the S-m-n Theorem (Theorem 2.1), there is a recursive g such that, for all i, 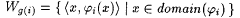 . Let GN be an index for N. Consider the scientist M that behaves as follows on each s : . Let GN be an index for N. Consider the scientist M that behaves as follows on each s : |
|
|
|
|
|
|
|
|
It is easy to verify that M is accountable on 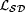 and that is identifies and that is identifies 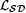 . . |
|
|
|
|
|
|
|
|
Now suppose by way of contradiction that an accountable scientist M identifies 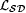 . Through an implicit use of Kleene's recursion theorem (Theorem 2.3), we exhibit a . Through an implicit use of Kleene's recursion theorem (Theorem 2.3), we exhibit a  which M fails to identify. We construct a text for this We in stages. which M fails to identify. We construct a text for this We in stages. |
|
|
|
|
|
|
|
|
Stage 0: s 0 = 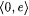 . . |
|
|
|
|