|
|
|
|
|
|
terminology will also be employed. We often identify a function f with its canonical text (and vice versa). Thus 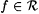 will denote both the function f as well as the canonical text for f. Moreover, f[n] will denote both the partial function will denote both the function f as well as the canonical text for f. Moreover, f[n] will denote both the partial function 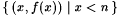 and the initial segment of length n of the canonical text for f. Context will determine which one is intended. The obvious analogue to Proposition 4.15 may also be recorded here (in which the Mi's represent machines with domain SEG). and the initial segment of length n of the canonical text for f. Context will determine which one is intended. The obvious analogue to Proposition 4.15 may also be recorded here (in which the Mi's represent machines with domain SEG). |
|
|
|
|
|
|
|
|
4.22 Proposition Let M0, M1, . . . be an enumeration of all (possibly partial) computable scientists. There is a total recursive 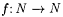 such that for all such that for all 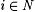 : : |
|
|
|
|
|
|
|
|
(b) For all 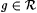 , if Mi identifies g then Mf(i) identities g. , if Mi identifies g then Mf(i) identities g. |
|
|
|
|
|
|
|
|
4.23 Corollary There exists a recursively enumerable sequence of total computable scientists M0, M1, . . ., such that 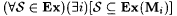 . . |
|
|
|
|
|
|
|
|
§4.3.2 Identifiability in Ex |
|
|
|
|
|
|
|
|
Proposition 3.43 shows that the identifiability problem has a trivial solution in the Func paradigm: every set of total recursive functions is identifiable. In contrast, identifiability within Ex is not such a simple affair, as we shall now see. Define two subsets of R as follows. |
|
|
|
|
|
|
|
|
4.24 Definition (a) SD is the set of all 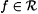 such that j f(0) = f. such that j f(0) = f. |
|
|
|
|
|
|
|
|
(b) A e Z is the set of all 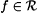 such that for all but finitely many such that for all but finitely many 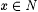 , f(x) = 0. , f(x) = 0. |
|
|
|
|
|
|
|
|
The symbol SD may be read as "self-describing." The symbol A e Z may be read as "almost everywhere zero." Lemma 2.4 shows that 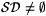 . . |
|
|
|
|
|
|
|
|
4.25 Theorem (The Nonunion Theorem, Blum and Blum [18]) 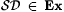 and and  , but , but 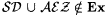 . . |
|
|
|
|
|
|
|
|
Proof: Exercise 4-10 shows that both SD and A e Z are in Ex. It remains to prove that  . So, suppose that computable scientist M identifies A e Z. By Proposition 4.22 we may assume without loss of generality that M is total. It suffices to . So, suppose that computable scientist M identifies A e Z. By Proposition 4.22 we may assume without loss of generality that M is total. It suffices to |
|
|
|
|