|
|
|
|
|
|
By M's memory limitation and the choice of m, 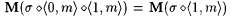 . So, again by M's memory limitation, . So, again by M's memory limitation, 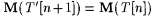 for all for all 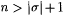 , that is, M converges on T' and T to the same index. But T' is a text for , that is, M converges on T' and T to the same index. But T' is a text for 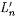 , T is a text for Ln, and , T is a text for Ln, and 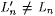 . Therefore M does not identify at least one of . Therefore M does not identify at least one of 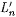 and Ln, contradicting our choice of M. and Ln, contradicting our choice of M. |
|
|
|
|
|
|
|
|
We shall see similar interactions with computability in later chapters. |
|
|
|
|
|
|
|
|
§4.2.5 Identifiability by Total Scientists |
|
|
|
|
|
|
|
|
The definitions of Section 3.4 do not require a scientist that identifies text T to be defined on every initial segment T[n] of T. However, there is little effect limiting attention to such scientists. Indeed, we can go further, and limit attention to scientists representing total functions from SEQ to N (hence defined on every initial segment of any environment). Scientists with this property are called "total," and suffice to identify any identifiable collection." This is shown by the following. |
|
|
|
|
|
|
|
|
4.15 Proposition Let M0, M1, . . . be an enumeration of all (possibly partial) computable scientists. There is total recursive 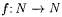 such that for all such that for all 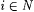 : : |
|
|
|
|
|
|
|
|
(b) For all 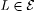 , if Mi identifies L then Mf(i) identifies L. , if Mi identifies L then Mf(i) identifies L. |
|
|
|
|
|
|
|
|
Proof: Given 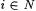 , we want Mf(i) to simulate Mi on , we want Mf(i) to simulate Mi on 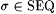 but not wait forever if but not wait forever if 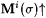 . Therefore, we will allow Mf(i) to wait only . Therefore, we will allow Mf(i) to wait only 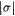 steps for steps for 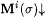 . Define: . Define: 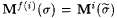 where where  is the longest initial segment of s such that is the longest initial segment of s such that 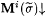 in in 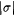 steps, if such exists; = 0 otherwise. steps, if such exists; = 0 otherwise. |
|
|
|
|
|
|
|
|
Mf(i) is computable because the condition defining  can be checked recursively (since the waiting time is bounded by can be checked recursively (since the waiting time is bounded by 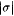 ). To see that Mf(i) identifies every language L that Mi does, let T be a text for such an L. Then there is ). To see that Mf(i) identifies every language L that Mi does, let T be a text for such an L. Then there is 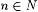 and index j for L such that for all and index j for L such that for all 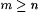 , Mi(T[m) = j. Let , Mi(T[m) = j. Let 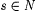 be the running time of Mi(T[n]). By the definition of Mf(i), if m exceeds both s and n, then Mf(i)(T[m]) = Mi(T[k]) for some be the running time of Mi(T[n]). By the definition of Mf(i), if m exceeds both s and n, then Mf(i)(T[m]) = Mi(T[k]) for some 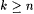 . Thus Mf(i) converges on T to j. . Thus Mf(i) converges on T to j. |
|
|
|
|
|
|
|
|
The foregoing proof uses two techniques that appear frequently within our theory. First, the scientist Mf(i) whose existence must be proved relies upon an internal simulation of the given scientist Mi. Mf(i) feeds Mi some version of the incoming data and then uses Mi's output for its own conjectures. Such proofs may be called "internal |
|
|
|
|