|
|
|
|
|
|
3.21 Definition Let s ,  be given. be given. |
|
|
|
|
|
|
|
|
(a) The result of concatenating  onto the end of s is denoted by onto the end of s is denoted by 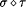 . Sometimes we abuse notation slightly and write . Sometimes we abuse notation slightly and write  (where (where 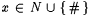 ) to denote the sequence formed by adding x at the end of s . ) to denote the sequence formed by adding x at the end of s . |
|
|
|
|
|
|
|
|
(b) We write "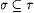 " if s is an initial segment of " if s is an initial segment of  , and " , and "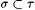 " if s is a proper initial segment of " if s is a proper initial segment of  . . |
|
|
|
|
|
|
|
|
(c) Likewise, we write 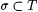 if s is an initial finite sequence of text T. if s is an initial finite sequence of text T. |
|
|
|
|
|
|
|
|
(d) Let finite sequences s 0, s 1, s 2 . . . be given such that 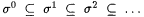 and and  . Then there is unique text T such that for all . Then there is unique text T such that for all  , , 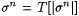 . This text is denoted . This text is denoted 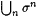 . . |
|
|
|
|
|
|
|
|
3.22 Theorem (Blum and Blum[18]) Suppose that scientist F identities 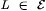 . Then there is . Then there is 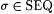 such that: such that: |
|
|
|
|
|
|
|
|
(a)  ; ; |
|
|
|
|
|
|
|
|
(c) for all 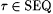 , if , if  , then , then 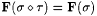 . . |
|
|
|
|
|
|
|
|
Proof (following Blum and Blum): Let scientist F and  be given. Without loss of generality, we assume that F is defined for all s . Assume that there is no be given. Without loss of generality, we assume that F is defined for all s . Assume that there is no 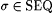 meeting conditions (a)-(c) of the proposition. This implies the following. meeting conditions (a)-(c) of the proposition. This implies the following. |
|
|
|
 |
|
|
|
|
3.23 For each 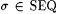 such that such that 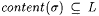 and WF( s ) = L, there is some and WF( s ) = L, there is some 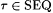 such that such that 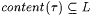 and and 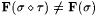 . . |
|
|
|
|
|
|
|
|
We show that 3.23 implies the existence of a text T for L which F does not identify. This proves the contrapositive of the theorem. |
|
|
|
|
|
|
|
|
Let U = u(0), u(1), u(2), . . . be an arbitrary text for L. We construct the promised text T in stages. At each stage n we specify a sequence s n such that 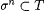 . . |
|
|
|
|
|
|
|
|
Stage  . Note that . Note that 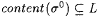 |
|
|
|
|
|
|
|
|
Stage n+1: Suppose that s n has been defined and that 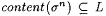 . There are two cases. . There are two cases. |
|
|
|
|
|
|
|
|
Case 1: 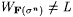 . Then . Then 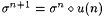 . . |
|
|
|
|