|
|
|
|
|
|
opposing point of view, see Putnam [156] and Pullum [154]). In any case we shall later consider paradigms that incorporate rationality requirements in one or another sense (see Chapter 5). |
|
|
|
|
|
|
|
|
Definition 3.12 is slightly different from the criterion of successful performance that we introduced informally in Section 1.3. Our earlier criterion required the learner to produce a last, correct guess, and to cease guessing thereafter. It thus corresponds to the following version of identification, here labeled ''identification*." |
|
|
|
|
|
|
|
|
3.16 Definition Scientist F identifies*  just in case for every text T for any just in case for every text T for any 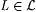 , , 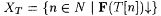 is finite and nonempty, and content(T) = WF(T[n) for the greatest is finite and nonempty, and content(T) = WF(T[n) for the greatest 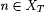 . In this case . In this case  is identifiable*. is identifiable*. |
|
|
|
|
|
|
|
|
The reader can easily verify that the two criteria of success are equivalent in the sense of the next proposition. |
|
|
|
|
|
|
|
|
3.17 Proposition 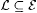 is identifiable if and only if is identifiable if and only if 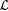 is identifiable*. is identifiable*. |
|
|
|
|
|
|
|
|
Identification* is one of many criteria that are transparently equivalent to identification; another is presented in Exercise 3-4. (Criteria that are not equivalent to identification arise in Chapter 6.) |
|
|
|
|
|
|
|
|
To close this section we record the identifiability of a collection of languages that. recalls the discussion of Section 1.3. |
|
|
|
|
|
|
|
|
3.18 Proposition Let  . Then . Then 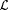 is identifiable. is identifiable. |
|
|
|
|
|
|
|
|
Proof: Given any 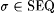 , let x s be the least , let x s be the least 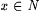 such that such that 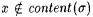 . Let scientist F be defined by the condition that for all . Let scientist F be defined by the condition that for all 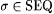 , F( s ) = the least index for N - { x s }. It is clear that F identifies , F( s ) = the least index for N - { x s }. It is clear that F identifies 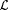 . . |
|
|
|
|
|
|
|
|
§3.5 Identification as a Limiting Process |
|
|
|
|
|
|
|
|
Let scientist F identify text T, and let 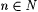 be given. We say that F "begins to identify T at moment n" just in case n is the least integer such that: be given. We say that F "begins to identify T at moment n" just in case n is the least integer such that: |
|
|
|
|
|
|
|
|
(a) 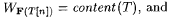 |
|
|
|
|
|
|
|
|
(b) 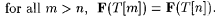 |
|
|
|
|