|
|
|
|
|
|
12-9 (Freivalds [61], Chen [37]) The following formalizes the notion of nearly minimal identification for functions. |
|
|
|
 |
|
|
|
|
12.29 Definition Let a be a member of (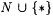 ) and let h be a recursive function. ) and let h be a recursive function. |
|
|
|
 |
|
|
|
|
(a) M 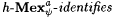 (written: (written: 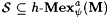 ) if and only if, for each ) if and only if, for each 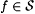 , we have that , we have that 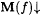 , y M(f) = a f, and , y M(f) = a f, and 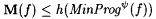 . . |
|
|
|
 |
|
|
|
|
(b) 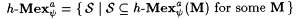 . . |
|
|
|
 |
|
|
|
|
(c) 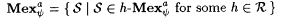 . . |
|
|
|
|
|
|
|
|
Thus, a scientist M 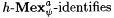 S just in case for each S just in case for each 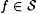 , M Exa-identifies f in the acceptable programming system y , and the final stabilized output of M on f is no bigger than h(MinProg y (f)). , M Exa-identifies f in the acceptable programming system y , and the final stabilized output of M on f is no bigger than h(MinProg y (f)). |
|
|
|
|
|
|
|
|
(a) Suppose that 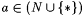 ) and that y and y ' are acceptable programming systems. Show that ) and that y and y ' are acceptable programming systems. Show that 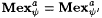 . (Thus, it makes sense to refer to . (Thus, it makes sense to refer to 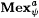 as just Mexa) as just Mexa) |
|
|
|
|
|
|
|
|
(b) Suppose that h is a recursive function such that, for all x, 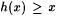 . Show that there exists an acceptable y such that for all S, . Show that there exists an acceptable y such that for all S, 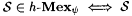 is finite. is finite. |
|
|
|
|
|
|
|
|
(c) Use part (b) and Exercise 12-7 to show that there are two acceptable programming systems y and y ' such that 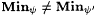 . . |
|
|
|
|
|
|
|
|
12-10 (Chen [37]) Show the following: |
|
|
|
|
|
|
|
|
(a) 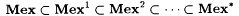 . . |
|
|
|
|
|
|
|
|
(b) For each 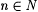 , , 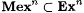 . . |
|
|
|
|
|
|
|
|
(c) 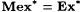 . . |
|
|
|
|
|
|
|
|
12-11 Using an argument similar to that for Proposition 12.15, prove: 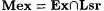 |
|
|
|
|
|
|
|
|
12-12 For each 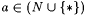 , define TxtMexa to the obvious variation on TxtMex that permits a-many anomalies in the final grammar. Show the following: , define TxtMexa to the obvious variation on TxtMex that permits a-many anomalies in the final grammar. Show the following: |
|
|
|
|
|
|
|
|
(a) 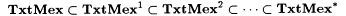 . . |
|
|
|
|
|
|
|
|
(b) For each 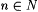 , , 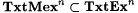 . . |
|
|
|
|
|
|
|
|
(c) 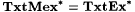 . . |
|
|
|
|