|
|
|
|
|
|
each element of S, but there is no scientist that infers an n-error program for each element of S—even if we allow the scientist to make an arbitrary number of mind changes. The proof of this proposition follows from the argument given for Proposition 6.5. |
|
|
|
|
|
|
|
|
12.2 Proposition (Case and Smith [35]) For each 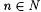 , ,  . . |
|
|
|
|
|
|
|
|
Similarly, as an immediate consequence Corollary 6.6, we have the following. |
|
|
|
|
|
|
|
|
12.3 Corollary (Case and Smith [35])  . . |
|
|
|
|
|
|
|
|
The next result shows the advantages of allowing an extra number of mind changes. The first part says that there is a collection of functions S for which there is a scientist that for each function in S infers a program via only n + 1 mind changes, but for which even a *-error program cannot be identified if only n mind changes are allowed |
|
|
|
|
|
|
|
|
12.4 Proposition (Case and Smith [35)] (a) 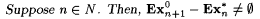 . . |
|
|
|
|
|
|
|
|
(b) 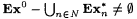 . . |
|
|
|
|
|
|
|
|
Proof: We argue only the special case of part (a): 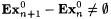 . Part (b) and the general case of part (a) are handled in Exercise 12-1. . Part (b) and the general case of part (a) are handled in Exercise 12-1. |
|
|
|
|
|
|
|
|
Let 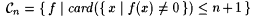 , which is clearly in Exn+1. Suppose by way of contradiction that there is an , which is clearly in Exn+1. Suppose by way of contradiction that there is an 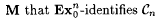 . Let . Let  , which is obviously in Cn. Hence, by our assumption on M, there is an , which is obviously in Cn. Hence, by our assumption on M, there is an |
|
|
|
|
|
|
|
|
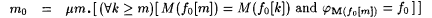 . . |
|
|
|
|
|
|
|
|
For i = 1, . . ., n + 1, we inductively define fi and mi as follows. |
|
|
|
|
|
|
|
|
It follows from a simple induction argument that each fi is a member of Cn, and thus that each mi is well defined. It also follows that M on fn+1 has a mind change at each of the n + 1 many points m1, . . ., mn+1, a contradiction. |
|
|
|
|