Page 229

		The first corollary says that if we fix the number of errors allowed in the additional information, then larger collections of functions can be Bex-identified by allowing extra errors in the final inferred program. This gain is achieved, however, only so far as the bound on the number of errors in the final inferred program does not exceed the bound on the number of errors allowed in the additional information. When these two bounds become equal, there is nothing to be gained by allowing extra errors in the final program. The second corollary says that, on the other hand, if a finite but unbounded number of errors is allowed in the additional information, allowing extra errors in the final program always yields a gain.

		Thus far we have concentrated on showing the advantage of allowing extra errors in the final inferred program. We now consider the effects of allowing extra errors in the additional information. The next result shows that there are collections of functions for which an accurate program can be UniBex-identified in the presence of an upper bound on the minimal size c-error program, but for which even a *-error program cannot be UniBex-identified in the presence of an upper bound on the minimal size (c + 1)-error program.

		10.12 Proposition For each , .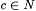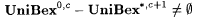

		Proof: Consider the following collections of functions:

		.

		.

		.

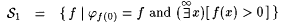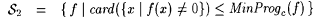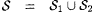		We exhibit a scientist M0 that UniBex0,c-identifies S. First we define an auxiliary function F such that, for any finite set D,

		Now, for each x and  s , define