|
|
|
|
|
|
6.9 Proposition (J. Steel cited in Case and Smith [35]) 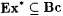 . . |
|
|
|
|
|
|
|
|
There remains the obvious question of whether Bc is strictly weaker than Ex*. The following proposition provides an affirmative answer. |
|
|
|
|
|
|
|
|
6.10 Proposition (Case and Smith [35]) 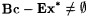 . . |
|
|
|
|
|
|
|
|
Proof: Let 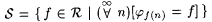 . Thus . Thus 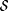 is the collection of computable functions f such that, for all but finitely many n, f(n) is an index for f. By Lemma 2.4, is the collection of computable functions f such that, for all but finitely many n, f(n) is an index for f. By Lemma 2.4, 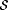 is nonempty. is nonempty. |
|
|
|
|
|
|
|
|
Clearly, 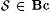 . Fix an arbitrary scientist M. Below we exhibit a function . Fix an arbitrary scientist M. Below we exhibit a function 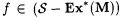 . It will thus follow that . It will thus follow that 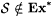 . Without loss of generality, we assume that M is total. . Without loss of generality, we assume that M is total. |
|
|
|
|
|
|
|
|
By the operator recursion theorem (Theorem 2.6), there is a 1-1, recursive function p such that the behavior of programs with indexes p(0), p(1), p(2), . . . are as described in stages below. We arrange things so that one of the j (i)'s witnesses the failure of M to 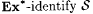 . . |
|
|
|
|
|
|
|
|
In the following construction 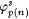 denotes the part of j p(n) defined before stage s. Let xs denote the least x such that j p(0) has not been defined before stage s. For each n, set denotes the part of j p(n) defined before stage s. Let xs denote the least x such that j p(0) has not been defined before stage s. For each n, set 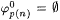 . If the construction reaches stage s, then the domain of . If the construction reaches stage s, then the domain of 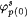 will be { 0, . . ., xs - 1 }, a finite initial segment of N, and will be { 0, . . ., xs - 1 }, a finite initial segment of N, and  and and 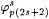 will be completely undefined. Go to stage 0. will be completely undefined. Go to stage 0. |
|
|
|
|
|
|
|
|
Let qs = M( j p(0)[xs]) and, for each x << xs, set j p(2s+1)(x) = j p(0)(x) and j p(2s+2)(x) = j p(0)(x). ( Hence, j p(0)[xs] = j p(2s+1)[xs] = j p(2s+2)[xs]. ) |
|
|
|
|
|
|
|
|
For y = xs to 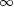 do do |
|
|
|
|
|
|
|
|
Set j p(2s+1)(y) = p(2s + 1) and j p(2s+2)(y) = p(2s + 2). |
|
|
|
 |
|
|
|
|
Condition 1. 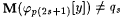 . .
Then, for each 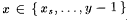 , set j p(0)(x) = j p(2s+1)(x) and henceforth make j p(2s+1) follow j p(0) so that p(2s + 1) is an index for j p(0). Go on to stage s + l. , set j p(0)(x) = j p(2s+1)(x) and henceforth make j p(2s+1) follow j p(0) so that p(2s + 1) is an index for j p(0). Go on to stage s + l. |
|
|
|
 |
|
|
|
|
Condition 2. Condition 1 fails, but 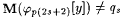 . .
Then, for each 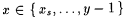 , set j p(0)(x) = j p(2s+2)(x) and, henceforth, make j p(2s+2) follow j p(0) so that p(2s + 2) is an index for j p(0). Go on to stage s + 1. ( Note that if neither condition succeeds, then the For loop continues. ) , set j p(0)(x) = j p(2s+2)(x) and, henceforth, make j p(2s+2) follow j p(0) so that p(2s + 2) is an index for j p(0). Go on to stage s + 1. ( Note that if neither condition succeeds, then the For loop continues. ) |
|
|
|
|