|
|
|
|
|
|
All of the extensions considered in b will be in 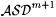 . If the search for a suitable extension succeeds in infinitely many stages, we then takef to be j e, which will turn out to belong to . If the search for a suitable extension succeeds in infinitely many stages, we then takef to be j e, which will turn out to belong to 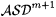 . But M on such an f fails to converge. On the other hand, if at some stage, no suitable extension can be found, then M converges to the same program, p, for each of the extensions considered in b. But in this case we arrange that, among these extensions, there is one that differs from j p on each of the m + 1-many arguments xs, . . ., xs + m; hence M fails to converge to an m-error index for that particular extension. . But M on such an f fails to converge. On the other hand, if at some stage, no suitable extension can be found, then M converges to the same program, p, for each of the extensions considered in b. But in this case we arrange that, among these extensions, there is one that differs from j p on each of the m + 1-many arguments xs, . . ., xs + m; hence M fails to converge to an m-error index for that particular extension. |
|
|
|
|
|
|
|
|
Here is the formal construction. |
|
|
|
|
|
|
|
|
Let j e(0) = e. Let xs denote the least x such that j e(x) has not been defined before stage s. Thus, x0 = 1. Go to stage 0. |
|
|
|
|
|
|
|
|
For each  , define the function fy as follows. , define the function fy as follows.
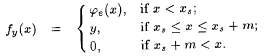 |
|
|
|
|
|
|
|
|
Dovetail between a and b below until, if ever, the search in b succeeds. |
|
|
|
 |
|
|
|
|
a. For i = l to 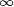 , set j e(xs + m + i) = 0. , set j e(xs + m + i) = 0.
b. Search for a 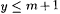 and an and an 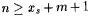 such that such that 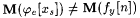 . . |
|
|
|
|
|
|
|
|
If and when the search in b succeeds, let y and n be as discovered in the search and set j e(x) = fy(x) for each x < n for which j e, has yet to be defined. ( Hence, j e [n] = fy [n]. )
Go on to stage s + 1. |
|
|
|
|
|
|
|
|
Consider the following two cases. |
|
|
|
|
|
|
|
|
Case 1: Infinitely many stages are executed. In this case, let f = j e. It is clear by construction that 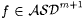 . But scientist M makes infinitely many mind changes on this f, hence M fails to Exm-identify f. . But scientist M makes infinitely many mind changes on this f, hence M fails to Exm-identify f. |
|
|
|
|
|
|
|
|
Case 2: Some stage s starts but never terminates. For each 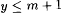 , let fy be as defined in stage s and let p = M( j e[xs]). By construction, for each y, , let fy be as defined in stage s and let p = M( j e[xs]). By construction, for each y,  . Also, since stage s never terminates, we have that, for each . Also, since stage s never terminates, we have that, for each 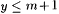 , ,  . But since . But since  , it follows that there is at least one , it follows that there is at least one 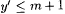 |
|
|
|
|