Enumerating strings from NFAs
If we want to use NFAs to reprsent (some aspect of) our grammatical knowledge, we need to be able to not just use them to determine whether an input is well-formed or not, but also to construct well-formed inputs.
Conceptually, each complete path through the machine represents a (possibly distinct) grammatical input. Thus the problem of constructing well-formed inputs reduces to the problem of finding a complete path through a machine.
It is useful to not only be able to construct a single well-formed input, but also every well-formed input. This is called enumerating the language of the grammar. An enumeration of the elements of a set is a (possibly) infinite list of elements such that each element in the set appears somewhere in the list. A special kind of enumeration is an enumeration without repetition. This is an enumeration where every element appears exactly once in the list.
Consider the machine in figure fig:NFA1.EnumStr.

Figure 1: A NFA accepting a word iff it has an odd number of as, and an even number of bs
Viewing this machine as a graph, we can ‘unfold’ it into a tree whose nodes are states, whose branches are transitions, and whose root is the start state. The first four levels of ‘unfolding’ is shown in figure fig:NFA1.Tree.EnumStr, where final states are circled.
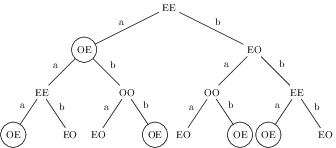
Figure 2: Partially unfolding the graph in figure fig:NFA1.EnumStr
Every possible path through the finite state machine starting at the initial state is represented in its unfolding. We can construct such a tree from a NFA by means of the following operation, which takes a state as argument, and produces a sequence of states paired with input strings as output.
> {-# LANGUAGE ExplicitForAll #-}
We have seen already how to define trees, I repeat the definition here
for completeness.
> data Tree a = Node a [Tree a]
Much like we can fold through a list, combining all of its entries
into a single output, we can do the same for a tree.
> foldTree :: (a -> [b] -> b) -> Tree a -> b
> foldTree combine = combineTree
> where
> combineTree (Node a ts) = a `combine` (map combineTree ts)
We can create a tree if we have
1. a function that takes a value, constructs a root label, and a list
of new values
2. a starting value
> unfoldTree :: (b -> (a,[b])) -> b -> Tree a
> unfoldTree grow = growTree
> where
> growTree seed = let (a,newSeeds) = grow seed
> in Node a (map growTree newSeeds)
We have seen many ways to define NFAs. I will chose this one for simplicity.
> data NFA q a = NFA
> q -- start state
> (q -> Bool) -- final states
> [(q,Maybe a,q)] -- list of transitions
Unfolding an NFA involves constructing a tree, so it is no surprise
that we use the tree construction function /unfoldTree/. The starting
value is the pair of the initial state and 'Nothing' - there is no
input needed to start at the initial state. The growth function puts
the seed as the root label, and the next seeds are the letters read
and next states of every transition starting with the state in the
current seed.
> unfoldNFA :: Eq q => NFA q a -> Tree (Maybe a,q)
> unfoldNFA (NFA qI isFinal tr) = unfoldTree f (Nothing,qI)
> where
> f seed@(ma,q) = let newSeeds = map dropFirst (filter (startsWith q) tr)
> in (seed,newSeeds)
> dropFirst (_,b,c) = (b,c)
> startsWith q (a,_,_) = q == a
In order to use our previous datatype, which doesn’t permit labeled branches, we have moved the label on the branches to inside the node.
But of course, we do not want to enumerate nodes of the tree (which correspond to states of the machine), but rather paths (i.e. words). Intuitively, we would like to move down through the tree, keeping track of the word built thus far at each node, and outputting it whenever we reach a final state. We see that we don’t really need to record the name of the state, only whether it is final or not. This yields us the tree in figure fig:NFA1.BetterTree.EnumStr.
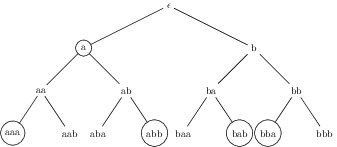
Figure 3: A better tree representation for generation
We can obtain such a representation from the one in figure fig:NFA1.Tree.EnumStr by
- changing the state to a boolean indicating whether it is final or not
- adding to each letter at a node the concatenation of all letters dominating it
Just as we can map a function over a list, changing each element in
the list while keeping the structure of the list the same, so too can
we map a function over a tree, changing the node values, while keeping
the shape of the tree the same.
> mapTree :: (a -> b) -> Tree a -> Tree b
> mapTree f = foldTree (Node . f)
When working with pairs, we will sometimes want to apply a function to
just one component of the pair.
> mapFst :: (a -> b) -> (a,c) -> (b,c)
> mapFst f (a,c) = (f a,c)
> mapSnd :: (a -> b) -> (c,a) -> (c,b)
> mapSnd f (c,a) = (c,f a)
As the states in our unfolded NFA trees are in the second component of
the pairs that label the nodes of the trees, changing states involves
mapping a function over the second component of the labels in our
trees.
> changeStateComponent = mapTree . mapSnd
I visualize the downward flow of information in a tree like a snowball
rolling down a mountain. This function changes a tree with
information b at its nodes into one with information c at its nodes.
It begins with a small snowball value, and begins rolling it down the
tree b. It uses a function which takes a snowball value and the
current root of the tree, and computes a new snowball value together
with the root of the new tree.
> avalanche :: (a -> b -> (a,c)) -> a -> Tree b -> Tree c
> avalanche roll = go
> where
> go snowball (Node b ts) = let (newSnowball,c) = snowball `roll` b
> in Node c (map (go newSnowball) ts)
Modifying the unfolded NFA tree is then just combining the state
component change with the input avalanche.
> modifyUnfoldedNFA :: NFA q a -> Tree (Maybe a,q) -> Tree ([a],Bool)
> modifyUnfoldedNFA (NFA _ isFinal _) =
> avalanche roll [] . changeStateComponent isFinal
> where
> roll str (Nothing,b) = (str,(str,b))
> roll str (Just a,b) = (a:str,(a:str,b))
Now each node corresponds to a string. We can enumerate nodes in a number of ways, but we have seen depth-first and breadth-first strategies already. The depth-first strategy explores all nodes in earlier daughters before moving on to subsequent daughters, and thus will fail to generate an enumeration, in the sense given above, in case the tree is infinite. The breadth-first strategy explores all nodes in order of their depth in the tree, and thus is guaranteed to explore each node in a tree at some finite point in time. Using a breadth-first strategy, we will end up enumerating the strings accepted by a finite state machine in order of increasing length.
This is a simple implementation of breadth first tree traversals,
suggested by Chris Okasaki (https://doi.org/10.1145/357766.351253).
Okasaki suggests using a /queue/ data structure to hold the subtrees
that have yet to be expanded. A queue is a FIFO (first-in first-out)
data structure, that acts like a line (british 'queue') at a
supermarket; you enter into the line, and wait your turn.
Importantly, new arrivals must go to the _end_ of the line. We can
describe this data structure by means of the type class =Queue=. A
queue must have three operations, /singleton/ makes a one-element
queue, /pop/ returns the next element together with the rest of the
queue (if it is not empty), and /append/ joins two queues together.
> class Queue q where
> singleton :: a -> q a
> pop :: q a -> Maybe (a,q a)
> append :: q a -> q a -> q a
> add :: a -> q a -> q a
> add a q = q `append` singleton a
I implement a queue as a list, which is very inefficient.
> instance Queue [] where
> singleton x = [x]
> pop [] = Nothing
> pop (x:xs) = Just (x,xs)
> append = (++)
Now we can write an implementation of breadth first enumeration using
our queue data structure. Note that I had to explicitly tell Haskell
which instance of the =Queue= typeclass to use (where I write
/singleton :: forall a. a -> [a]/).
> bfQ :: Tree a -> [a]
> bfQ t = bfs ((singleton :: forall a. a -> [a]) t)
> where
> bfs q = case pop q of
> Nothing -> []
> Just (Node a ts,q') -> a : bfs (q' `append` ts)
Another conceptually very different way to implement breadth first
traversals is by first splitting the tree up into the lists of nodes
at each level, and then concatenating these lists together:
> bfL = concat . levels
Both of these operations are built-in; /concat/ is in the Prelude, and
/levels/ is in Data.Tree. In Data.Tree, there are two functions
/root/ and /subForest/ which return the root and the list of daughters
of an input tree:
> root (Node a _) = a
> subForest (Node _ ts) = ts
If we have a list of trees, then taking each of their subForests gives
us a list of list of trees (the list of lists of daughters), and then
concatenating them gives the list of trees which were the daughters of
the original trees. Iterating this some number of times, we can
obtain the lists of (grand-)*daughters of our tree, at any depth.
Once we have a list of (grand-)*daughters, we can obtain the list of
nodes at that depth by taking each of their roots! The function
levels, then, works by constructing the lists of daughters of the tree
at /every/ depth, and then taking the roots of each such list.
> levels t =
> map (map root)
> $ takeWhile (not . null)
> $ iterate (concatMap subForest) [t]
Enumeration of an NFA involves constructing the unfolded NFA,
modifying its nodes as described above, enumerating them, and throwing
away all strings not associated with a final state. We need to
reverse the strings that come out because I built them up backwards.
> enumerateNFA :: Eq q => NFA q a -> [[a]]
> enumerateNFA nfa = map reverse
> $ map fst
> $ filter snd
> $ bfL
> $ modifyUnfoldedNFA nfa
> $ unfoldNFA nfa
Finally, we can use the following machine to test the above code.
This machine accepts a string of booleans just in case there are an
even number of the symbol 'True'.
> evenTrue :: NFA Bool Bool
> evenTrue = NFA True id
> [(True,Just True,False)
> ,(True,Just False,True)
> ,(False,Just True,True)
> ,(False,Just False,False)]
We ask for the first ten sentences (in order of length) accepted by the machine.
λ> take 10 $ enumerateNFA evenTrue
[[],[False],[True,True],[False,False],[True,True,False],[True,False,True],[False,True,True],[False,False,False],[True,True,True,True],[True,True,False,False]]