Quantum field theory in curved spacetime (QFTCS) is the theory of quantum fields propagating in a background, classical, curved spacetime. On account of its classical treatment of the metric, QFTCS cannot be a fundamental theory of nature. However, QFTCS is expected to provide an accurate description of quantum phenomena in a regime where the effects of curved spacetime may be significant, but effects of quantum gravity itself may be neglected. In particular, it is expected that QFTCS should be applicable to the description of quantum phenomena occurring in the early universe and near (and inside of) black holes—provided that one does not attempt to describe phenomena occurring so near to singularities that curvatures reach Planckian scales and the quantum nature of the spacetime metric would have to be taken into account.
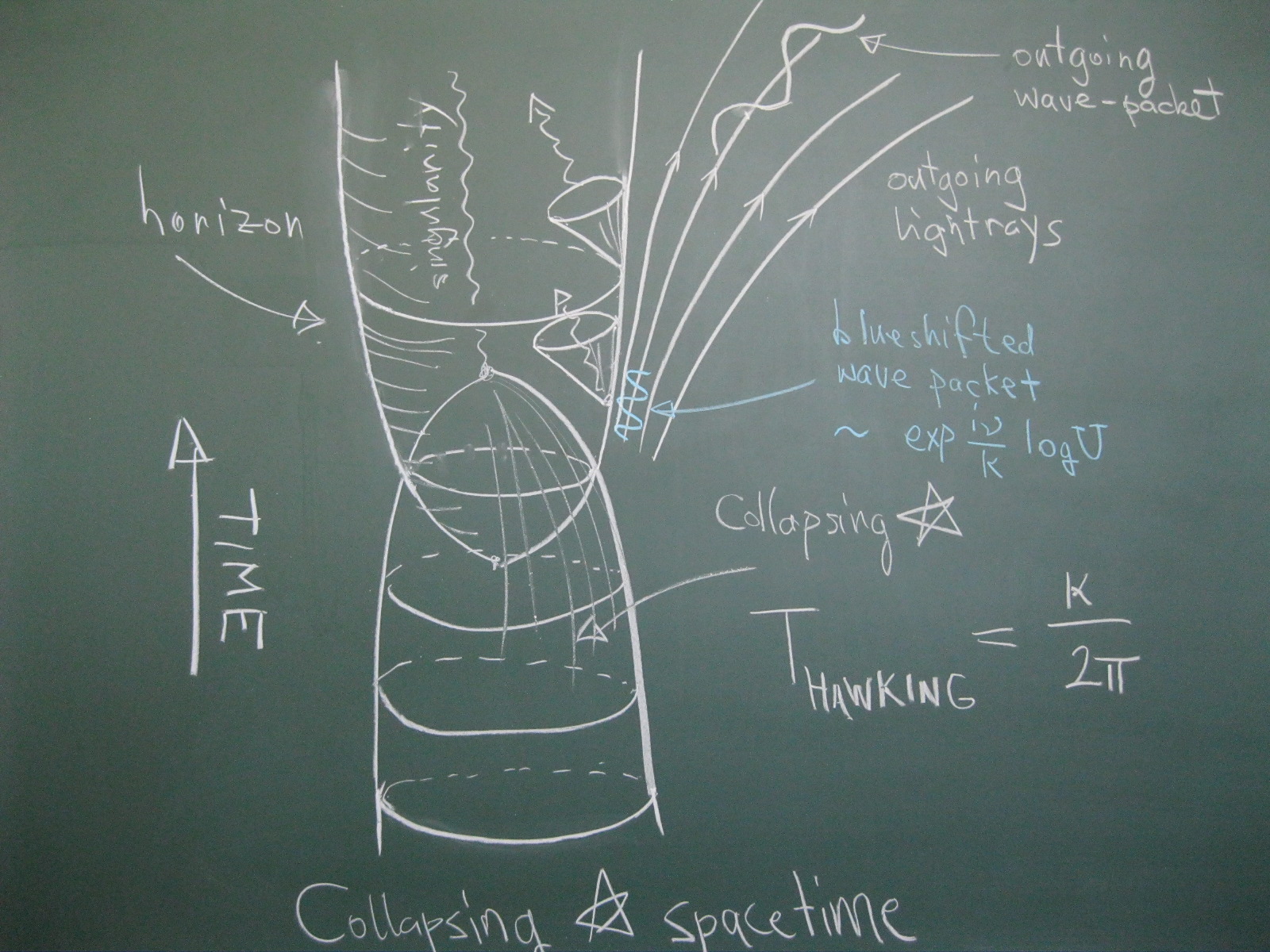
Quantum field theory in curved spacetimes has provided important physical insights into the quantum nature of black holes, indicating that they should, if left alone, gradually evaporate due to the emission of quanta whose energies are distributed thermally at the famous Hawking temperature, which is $= \kappa/2\pi$ in terms of the “surface gravity”, $\kappa$, of the black hole. For a Schwarzschild black hole, this would be
$$T_{\rm Hawking} = \frac{1}{8\pi M}$$
where $M$ is the mass of the black hole in geometrized units. These ideas continue to inspire current research, as for example the ongoing discussions about related issues like the “information loss paradox” show.
A second major physical effect, whose nature can in fact be seen to be closely tied to the Hawking effect, is the generation of quantum primordial fluctuations in the early Universe. These fluctuations are an illustration of the — at first very counterintuitive — fact that quantum effects “do not have to be small”. Indeed, the explanation of QFTCS is that tiny quantum fluctuations of the quantum fields that were present in the early Universe have been amplified by the expansion of the Universe to a colossal size — so much that they could actually serve as the seeds for the formation of structure in our cosmos. In this sense, it can be said that the distribution of structure on large scales (clusters of galaxies) is an imprint of quantum fluctuations in the early cosmos!
Apart from these important applications which continue to be explored today, QFTCS has also contributed to a much better understanding of the mathematical structures and physical principles underlying quantum field theory in general, by forcing one to think about quantum field theory in a “covariant manner”. It is very important to determine if quantum field theory can be given a mathematically precise and consistent formulation as a theory in its own right—and to provide such a formulation if it can be given. This is not because one believes that quantum field theory should be a “final” theory of nature; indeed, one does not believe that a quantum theory of the spacetime metric can be formulated within the existing framework of quantum field theory. However, even if quantum field theory has only a limited domain of validity, it is important to understand precisely what questions are well posed within its framework and how the answers to these questions are to be obtained. In this way, the predictions of quantum field theory can be made with clarity and precision, and hints may be provided for some of the features that might be expected to survive in a more fundamental theory that supersedes quantum field theory.
One fundamental insight into QFTCS is that there is, in general, no analogue of a preferred vacuum state. The point is not that it would be impossible to construct, in concrete examples, many states of special physical interest, but rather that it is not possible in general to single out a canonical preferred state for each spacetime. In this sense, one needs a formalism that establishes, a priori, a kind of ‘democracy’ between states, and that formulates the theory in terms of the elements that independent of any particular choices. It turns out that, in some sense, the right way to think about these theories is to emphasise the algebraic relations between the quantum fields, which are a structure that holds in any state. An example of an algebraic relation for a linear Klein-Gordon quantum field theory is the covariant commutation relation
$$[\phi(x_1), \phi(x_2)] = i \Delta(x_1, x_2) I \ ,$$
where $\Delta$ is the advanced minus the retarded Greens function for the Klein-Gordon operator $\square_g – m^2$ for the given spacetime. Another relation is the field equation itself, $(\square_g – m^2)\phi(x)=0$. Normally, quantum fields are defined as operators on a Hilbert-space, which contains the “vacuum” together with the excited “particle states”. Since there is no preferred vacuum in a curved spacetime, it is best to think about the relations such as those given above as generating an abstract algebra. If we want to discuss physical situations, we need to find representations of this abstract algebra on a Hilbert space of states. An important phenomenon that comes up in this context, and which is unfamiliar from quantum mechanics, is that different representations (i.e. different Hilbert spaces built on different “vacua”) can fail to be equivalent, i.e. one “vacuum” looks as if it contains infinitely many “particles” relative to the other — so many in fact that it fails to be represented by a normalizable density matrix in the Hilbert space of the other vacuum. This is another reason why it is advantageous to present the theory first in terms of its abstract relations.
For interacting quantum field theories, it is no longer so straightforward to write down the relations. This is not surprising, because the algebraic relations encode the information about the — in general very complicated — dynamics of the theory. But there is a way to produce this relations by means of the so-called “operator product expansion”. Alternatively, one can try to produce the abstract algebra of interacting fields by presenting their generators (“interacting fields”) in terms of perturbation expansions. In both cases, the algebraic relations/constructions turn out to be “covariant” and “local” in an appropriate sense. The algebraic relations also allow one to read off some fundamental symmetries such as PCT. Of course, in concrete spacetimes, in order to study concrete physical effects, one needs to find particular states/representations, and compute e.g. the correlation functions of the interacting fields in those states. This is a very difficult problem in general, but progress can be made e.g. for the highly symmetric cousin of Minkowski space with negative curvature, namely the so-called “deSitter spacetime”. Some further description of these topics may be obtained by following these links.