DeSitter spacetime is an important background in cosmology, because it is thought to describe both inflation, as well as the recent epoch of accelerated expansion. The deSitter metric is
\begin{equation}
ds^2 = -dt^2 +a(t)^2 (dx^2 + dy^2 + dz^2)
\end{equation}
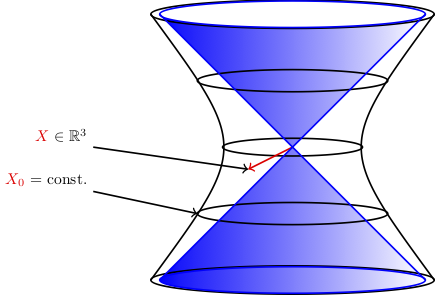
with an exponential expansion factor $a(t) = e^{tH}$. $H$ is called the “Hubble parameter”. Its value then, expressed in terms of energy, was on the order of the scale of elementary particles, whereas it is very tiny today. One of the attractions of deSitter space — apart from its obvious physical significance — is that it is a “maximally symmetric” spacetime. A way of representing deSitter space such that its symmetries are manifest is the following. Consider an auxiliary 5-dimensional Minkowskian embedding spacetime. Then deSitter can be viewed as the time-like hyperboloid of “radius” $H^{-2}$, and the group of isometries is obviously $O(4,1)$. The following pictures provide an illustration of this for the analog of 2-dimensional deSitter (embedded into $\mathbb{R}^3$).
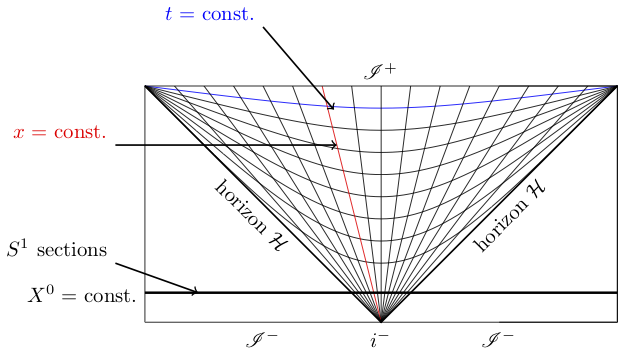
The part of deSitter spacetime covered by the original coordinates $t,x,y,z$ above is best visualized in a conformal diagram, drawn here for the case of 2-dimensional deSitter spacetime for the sake of easier visualisation. The diagram is obtained by cutting up the hyperboloid and applying a conformal transformation. The opposite vertical lines hence should be identified:
In the context of cosmology, it is of considerable interest to understand quantum fields on this background, because their fluctuations are directly tied e.g. to the power spectrum of the CMB. Concretely, these are encoded in the correlation functions $\langle \Omega, \phi(x_1) … \phi(x_n) \Omega \rangle$ in a suitable state $\Omega$. One natural choice of the state is the deSitter invariant “vacuum”, which exists e.g. for free scalar fields of positive mass $m$. In that case, the correlation functions can be found exactly. For self-interacting Klein-Gordon fields, such as e.g. $\phi^4$-theory, the correlation functions can be determined perturbatively.
A natural, and physically important, question is how the correlation functions behave for more general states, such as a state of the form $\Psi =\phi(f_1) … \phi(f_k) \Omega$, where the notation $\phi(f_i)$ indicates that we are averaging $\phi$ against some smooth function $f_i$. Of particular interest is what is the behavior of the correlation functions such as $\langle \Psi, \phi(x_1) \phi(x_2) \Psi \rangle$ for $x_1, x_2$ going to future infinity. The analysis if this question boils down to the study of the IR-properties of the deSitter invariant state $\Omega$, i.e. how its correlation functions behave for large proper times. This analysis has been carried out for self-interacting KG-fields. It leads to the following “quantum no-hair theorem”, which qualitatively states:
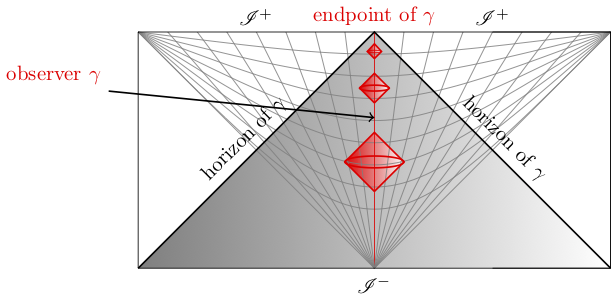
The proper way to interpret the theorem is that, within any causal diamond of fixed proper size, any state “looks” increasingly like the vacuum if the diamond is shifted towards the future, see figure.
Some references:
